《统计学习方法》第 14 章聚类方法 KMeans

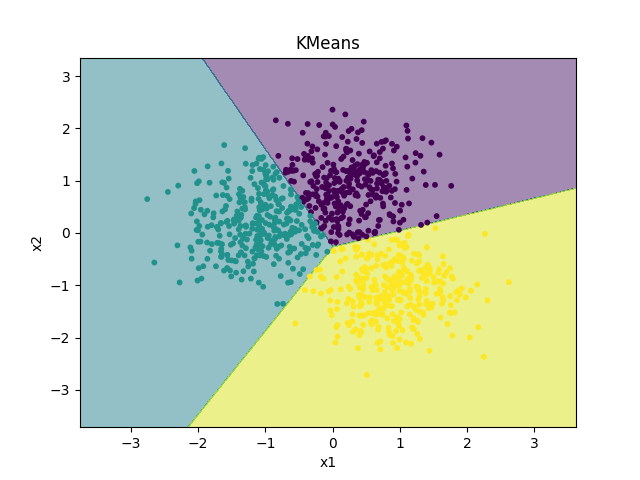
k-均值聚类

n 个样本分到 k 个不同的类或簇，每个样本到其所属类的中心的距离最小。

每个样本只能属于一个类，所有 k-均值聚类 是 硬聚类。

模型

k < n

$G_{i} \cap G_{j} = \varnothing, \bigcup_{i=1}^{k}G_{i} = X$

策略

距离：欧式距离
损失函数：样本与所属类的中心的距离总保
NP 困难问题

算法

目标函数极小化

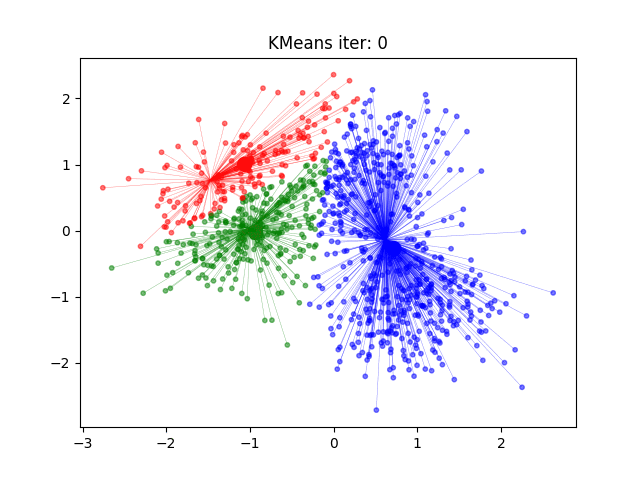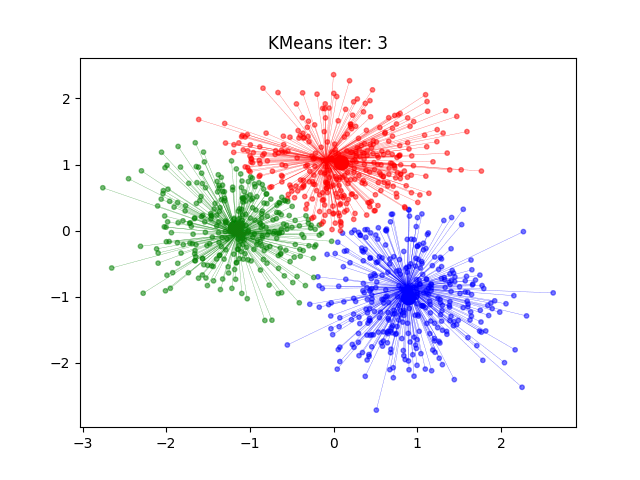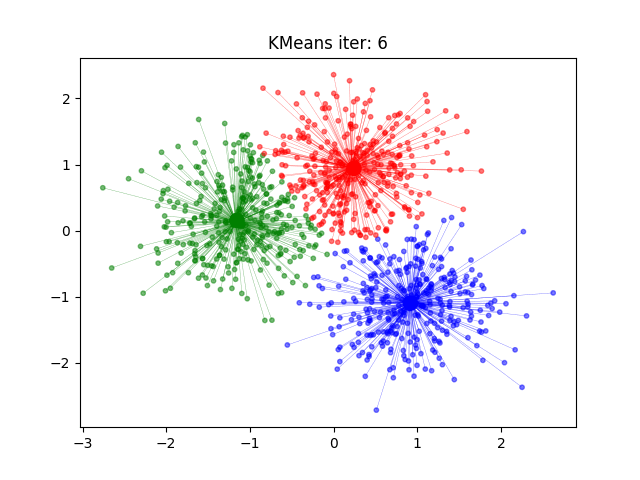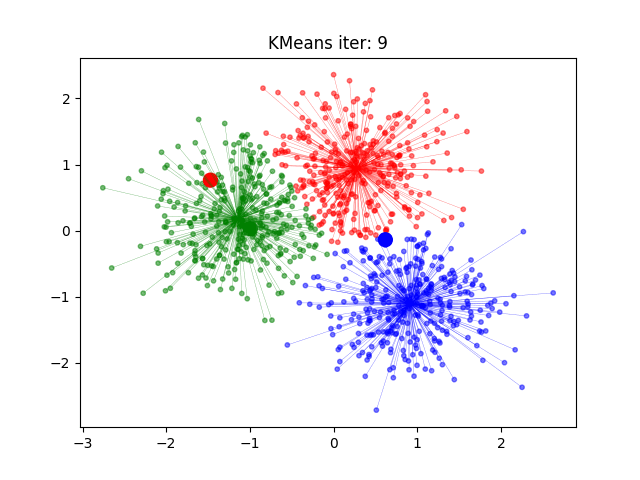
初始化，随机取 $ k $ 个样本做中心
对样本进行聚类，计算样本到类中心距离，每个样本指派到与其最近的中心的类
计算新的类中心。对聚类结果计算样本的均值，做为新的类中心
如果迭代收敛或符合停止条件，输出。否则，令 $ t = t + 1 $ ，返回 2

def fit(self, X):
    self._setup_input(X)
    n_samples, _ = X.shape
    # 从 X 中随机获取 k 个元素做中心
    self._centers = np.array(
        random.sample(list(np.unique(X, axis=0)), self.k))

    old_clusters = None
    n_iters = 0

    while True:
        new_clusters = [self._min_k(x) for x in X]

        if new_clusters == old_clusters:
            print("Training finished after {n_iters} iterations!".format(n_iters=n_iters))
            return

        old_clusters = new_clusters
        n_iters += 1

        for cluster_i in range(self.k):
            # 计算新的中心
            points_idx = np.where(np.array(new_clusters) == cluster_i)
            xi = X[points_idx]
            self._centers[cluster_i] = xi.mean(axis=0)

        self._centers_list.append(np.copy(self._centers))

源码：https://github.com/iOSDevLog/slmethod