Numpy 基础

Numpy 简介

Numpy

Numpy 库是 Python 中科学计算的核心库。它提供了高性能的多维数组对象以及用于处理这些数组的工具。

使用以下约定导入 Numpy

1	import numpy as np

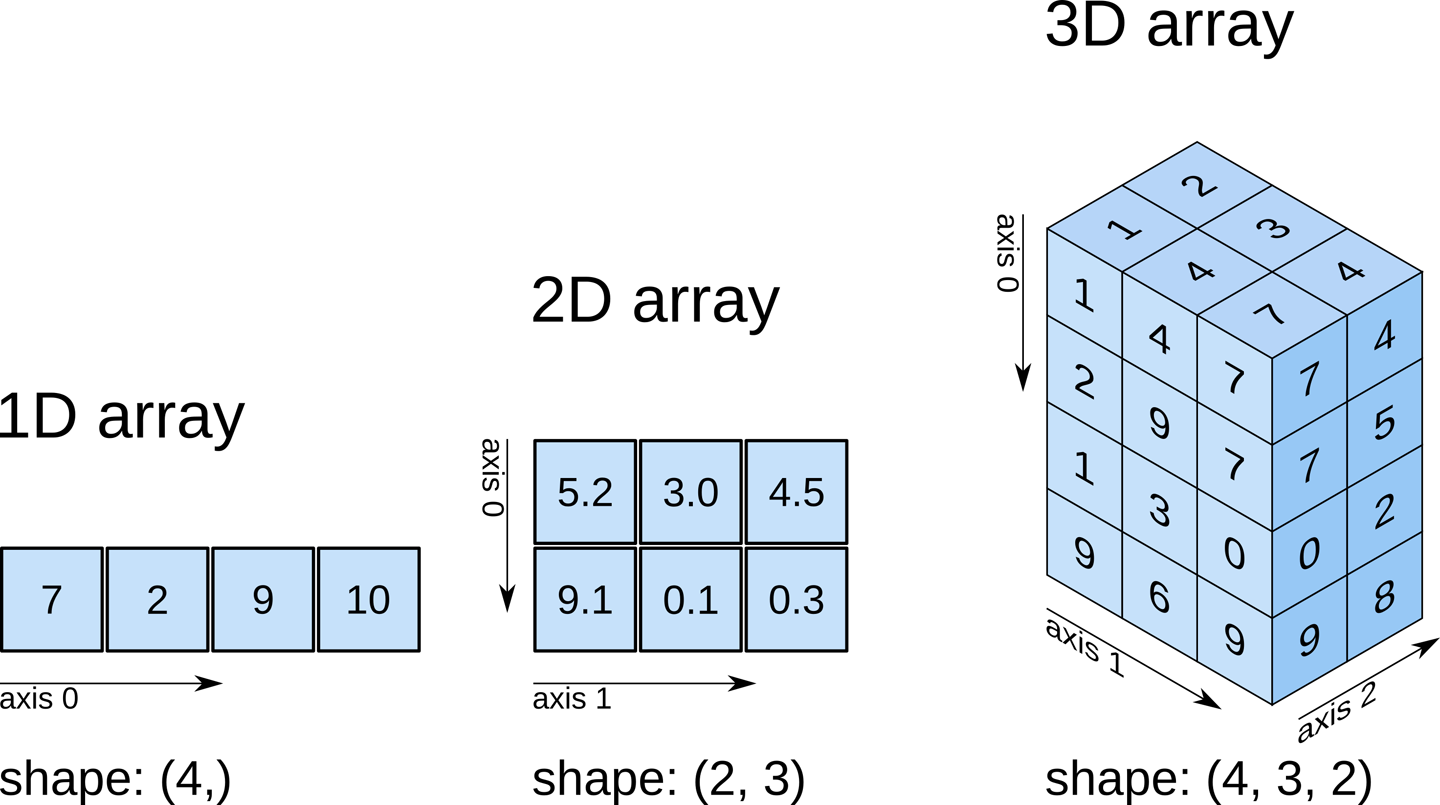
Numpy 数组

Numpy Array

帮助

1	np.info(np.ndarray.dtype)

创建数组

a = np.array([1,2,3])
b = np.array([(1.5,2,3), (4,5,6)], dtype = float)
c = np.array([[(1.5,2,3), (4,5,6)], [(3,2,1), (4,5,6)]],
dtype = float)

初始占位符

1 2	# 创建一个零数组 np.zeros((3,4))

array([[0., 0., 0., 0.],
[0., 0., 0., 0.],
[0., 0., 0., 0.]])

1 2	# 创建一个数组 np.ones((2,3,4), dtype=np.int16)

array([[[1, 1, 1, 1],
[1, 1, 1, 1],
[1, 1, 1, 1]],

[[1, 1, 1, 1],
[1, 1, 1, 1],
[1, 1, 1, 1]]], dtype=int16)

1 2	# 创建均匀间隔值的数组（步长值） d = np.arange(10,25,5)

1 2	# 创建均匀间隔值的数组（样本数） np.linspace(0,2,9)

array([0. , 0.25, 0.5 , 0.75, 1. , 1.25, 1.5 , 1.75, 2. ])

1 2	# 创建常量数组 e = np.full((2,2),7)

1 2	# 创建2X2单位矩阵 f = np.eye(2)

1 2	# 创建具有随机值的数组 np.random.random((2,2))

array([[0.64234353, 0.07179718],
[0.7937333 , 0.13764298]])

1 2	# 创建一个空数组 np.empty((3,2))

array([[0., 0.],
[0., 0.],
[0., 0.]])

文件 I / O

在磁盘上保存 & 加载

1
2
3

np.save('my_array', a)
np.savez('array.npz', a, b)
np.load('my_array.npy')

array([1, 2, 3])

保存 & 加载文本文件

1
2
3

np.loadtxt("myfile.txt")
np.genfromtxt("my_file.csv", delimiter=',')
np.savetxt("myarray.txt", a, delimiter=" ")

数据类型

1 2	# 有符号的64位整数类型 np.int64

numpy.int64

1 2	# 标准双精度浮点复数 np.float32

numpy.float32

1 2	# 由128浮点数表示的布尔类型 np.complex

complex

1 2	# 存储TRUE和FALSE np.bool

bool

1 2	# 值Python对象类型 np.object

object

1 2	# 固定长度的字符串类型 np.string_

numpy.bytes_

1 2	# 固定长度的unicode类型 np.unicode_

numpy.str_

检查数组

1 2	# 数组尺寸 a.shape

(3,)

1 2	# 数组长度 len(a)

1 2	# 数组维数 b.ndim

1 2	# 数组元素的数量 e.size

1 2	# 数组元素的数据类型 b.dtype

dtype(‘float64’)

1 2	# 数据类型的名称 b.dtype.name

‘float64’

1 2	# 将数组转换为其他类型 b.astype(int)

array([[1, 2, 3],
[4, 5, 6]])

数学运算

算术运算

1
2
3

# 减法
g = a - b
g

array([[-0.5, 0. , 0. ],
[-3. , -3. , -3. ]])

1 2	# 减法 np.subtract(a,b)

array([[-0.5, 0. , 0. ],
[-3. , -3. , -3. ]])

1 2	# 加法 b + a

array([[2.5, 4. , 6. ],
[5. , 7. , 9. ]])

1 2	# 加法 np.add(b,a)

array([[2.5, 4. , 6. ],
[5. , 7. , 9. ]])

1 2	# 乘法 a * b

array([[ 1.5, 4. , 9. ],
[ 4. , 10. , 18. ]])

1 2	# 除法 a / b

array([[0.66666667, 1. , 1. ],
[0.25 , 0.4 , 0.5 ]])

1 2	# 幂 np.multiply(a,b)

array([[ 1.5, 4. , 9. ],
[ 4. , 10. , 18. ]])

1 2	# 平方根 np.sqrt(b)

array([[1.22474487, 1.41421356, 1.73205081],
[2. , 2.23606798, 2.44948974]])

1 2	# 正弦 np.sin(a)

array([0.84147098, 0.90929743, 0.14112001])

1 2	# 余弦 np.cos(b)

array([[ 0.0707372 , -0.41614684, -0.9899925 ],
[-0.65364362, 0.28366219, 0.96017029]])

1 2	# 自然对数 np.log(a)

array([0. , 0.69314718, 1.09861229])

1 2	# 点积 e.dot(f)

array([[7., 7.],
[7., 7.]])

比较

1 2	# 元素比较 a == b

array([[False, True, True],
[False, False, False]])

1 2	# 元素比较 a < 2

array([ True, False, False])

1 2	# 数组比较 np.array_equal(a, b)

False

聚合函数

1 2	# 数组式和 a.sum()

1 2	# 数组最小值 a.min()

1 2	# 数组行的最大值 b.max(axis=0)

array([4., 5., 6.])

1 2	# 元素的累积总和 b.cumsum(axis=1)

array([[ 1.5, 3.5, 6.5],
[ 4. , 9. , 15. ]])

1 2	# 均值 a.mean()

2.0

1 2	# 中位数 np.median(b)

3.5

1 2	# 相关系数 np.corrcoef(a, b)

array([[1. , 0.98198051, 1. ],
[0.98198051, 1. , 0.98198051],
[1. , 0.98198051, 1. ]])

1 2	# 标准差 np.std(b)

1.5920810978785667

复制数组

1
2
3

# 使用相同的数据创建数组视图
h = a.view()
h

array([1, 2, 3])

1 2	# 创建数组的副本 np.copy(a)

array([1, 2, 3])

1
2
3

# 创建数组的深层副本
h = a.copy()
h

array([1, 2, 3])

排序数组

1
2
3

# 对数组进行排序
a.sort()
a

array([1, 2, 3])

1
2
3

# 对数组轴的元素进行排序
c.sort(axis=0)
c

array([[[1.5, 2. , 1. ],
[4. , 5. , 6. ]],
[[3. , 2. , 3. ],
[4. , 5. , 6. ]]])

切片与索引

下标

a[2]

b[1,2]

6.0

切片

a[:2]

array([1, 2])

b[0:2,1]

array([2., 5.])

b[:1]

array([[1.5, 2. , 3. ]])

c[1, ...]

array([[3., 2., 3.],
[4., 5., 6.]])

a[ : :-1]

array([3, 2, 1])

布尔索引

a[a<2]

array([1])

1 2	# 花式索引 b[[1, 0, 1, 0],[0, 1, 2, 0]]

array([4. , 2. , 6. , 1.5])

1	b[[1, 0, 1, 0]][:,[0,1,2,0]]

array([[4. , 5. , 6. , 4. ],
[1.5, 2. , 3. , 1.5],
[4. , 5. , 6. , 4. ],
[1.5, 2. , 3. , 1.5]])

数组操作

转置数组

1 2	# 重新排列数组维度 i = np.transpose(b)

1 2	# 重新排列数组维度 i.T

array([[1.5, 2. , 3. ],
[4. , 5. , 6. ]])

改变形状

1 2	# 展平数组 b.ravel()

array([1.5, 2. , 3. , 4. , 5. , 6. ])

1	g.reshape(3, -2)

array([[-0.5, 0. ],
[ 0. , -3. ],
[-3. , -3. ]])

添加 / 删除元素

1
2
3

# 返回一个形状为新的数组（2,6）
h = np.array([1, 2, 3])
h.resize((2, 6))

1 2	# 将元素附加到数组 np.append(h, g)

array([ 1. , 2. , 3. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. ,

, -0.5, 0. , 0. , -3. , -3. , -3. ])

1 2	# 在数组中插入元素 np.insert(a, 1, 5)

array([1, 5, 2, 3])

1 2	# 从数组中删除元素 np.delete(a,[1])

array([1, 3])

结合数组

1 2	# 连接数组 np.concatenate((a,d),axis=0)

array([ 1, 2, 3, 10, 15, 20])

1 2	# 垂直堆叠数组（逐行） np.vstack((a,b))

array([[1. , 2. , 3. ],
[1.5, 2. , 3. ],
[4. , 5. , 6. ]])

1 2	# 垂直堆叠数组（逐行） np.r_[e,f]

array([[7., 7.],
[7., 7.],
[1., 0.],
[0., 1.]])

1 2	# 水平堆叠阵列（逐列） np.hstack((e,f))

array([[7., 7., 1., 0.],
[7., 7., 0., 1.]])

1 2	# 创建堆叠的列式数组 np.column_stack((a,d))

array([[ 1, 10],
[ 2, 15],
[ 3, 20]])

1 2	# 创建堆叠的列式数组 np.c_[a,d]

array([[ 1, 10],
[ 2, 15],
[ 3, 20]])

分割数组

1 2	# 在第3个索引处水平拆分数组 np.hsplit(a,3)

[array([1]), array([2]), array([3])]

1 2	h h.resize(2, 6)

1 2	# 在第 2 个索引处垂直拆分数组 np.vsplit(c,2)

[array([[[1.5, 2. , 1. ],
[4. , 5. , 6. ]]]), array([[[3., 2., 3.],
[4., 5., 6.]]])]