卷积

运算的定义、动机（稀疏权重、参数共享、等变表示）

定义

函数 $f, g$ 是定义在 $\mathbb{R}^{n}$ 上的可测函数（measurable function），$f$ 与 $g$ 的卷积记作 $f * g$，它是其中一个函数翻转并平移后与另一个函数的乘积的积分，是一个对平移量的函数，也就是：

$(f * g)(t) \stackrel{\mathrm{def}}{=} \int_{\mathbb{R}^{n}} f(\tau) g(t-\tau) d \tau$

如果函数不是定义在 $\mathbb{R}^{n}$ 上，可以把函数定义域以外的值都规定成零，这样就变成一个定义在 $\mathbb{R}^{n} $ 上的函数。

图解卷积

卷积动画

Blue maps are inputs, and cyan maps are outputs.

注意：蓝色地图是输入，青色地图是输出。



No padding, no strides	Arbitrary padding, no strides	Half padding, no strides	Full padding, no strides

No padding, strides	Padding, strides	Padding, strides (odd)

一维卷积运算和二维卷积运算

反卷积(tf.nn.conv2d_transpose)

反卷积(转置卷积)动画

Blue maps are inputs, and cyan maps are outputs.

注意：蓝色地图是输入，青色地图是输出。



No padding, no strides, transposed	Arbitrary padding, no strides, transposed	Half padding, no strides, transposed	Full padding, no strides, transposed

No padding, strides, transposed	Padding, strides, transposed	Padding, strides, transposed (odd)

池化

在通过卷积获得了特征 (features) 之后，下一步我们希望利用这些特征去做分类。理论上讲，人们可以用所有提取得到的特征去训练分类器，例如 softmax 分类器，但这样做面临计算量的挑战。例如：对于一个 $96X96$ 像素的图像，假设我们已经学习得到了$400$个定义在$8X8$输入上的特征，每一个特征和图像卷积都会得到一个 $(96 − 8 + 1) * (96 − 8 + 1) = 7921$ 维的卷积特征，由于有 $400$ 个特征，所以每个样例 (example) 都会得到一个 $892 * 400 = 3,168,400$ 维的卷积特征向量。学习一个拥有超过 3 百万特征输入的分类器十分不便，并且容易出现过拟合 (over-fitting)。

为了解决这个问题，首先回忆一下，我们之所以决定使用卷积后的特征是因为图像具有一种“静态性”的属性，这也就意味着在一个图像区域有用的特征极有可能在另一个区域同样适用。因此，为了描述大的图像，一个很自然的想法就是对不同位置的特征进行聚合统计，例如，人们可以计算图像一个区域上的某个特定特征的平均值 (或最大值)。这些概要统计特征不仅具有低得多的维度 (相比使用所有提取得到的特征)，同时还会改善结果(不容易过拟合)。这种聚合的操作就叫做池化 (pooling)，有时也称为平均池化或者最大池化 (取决于计算池化的方法)。

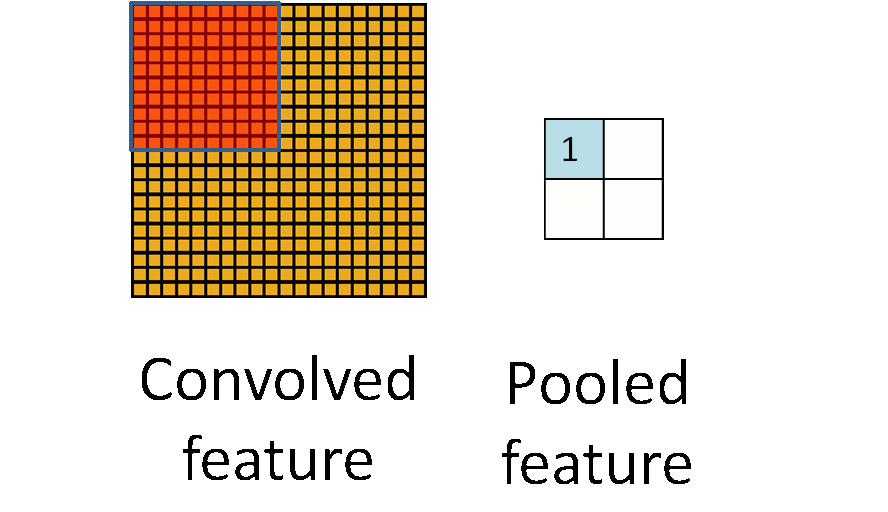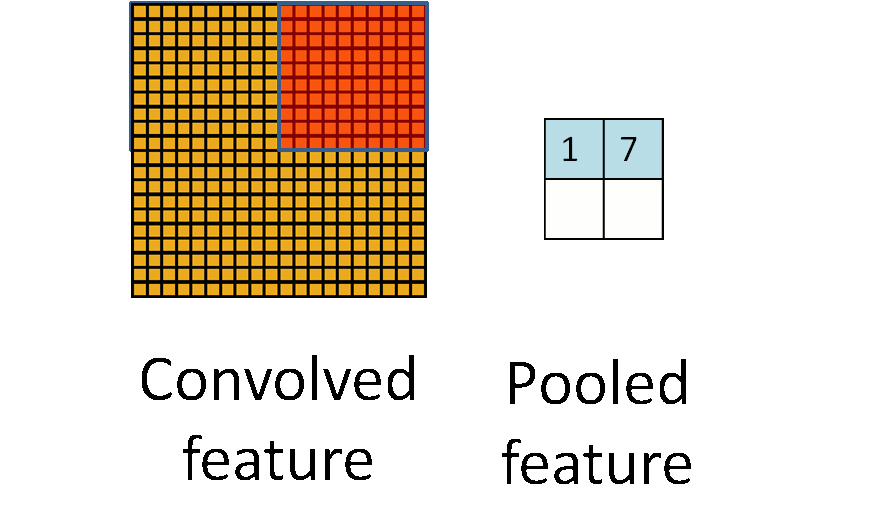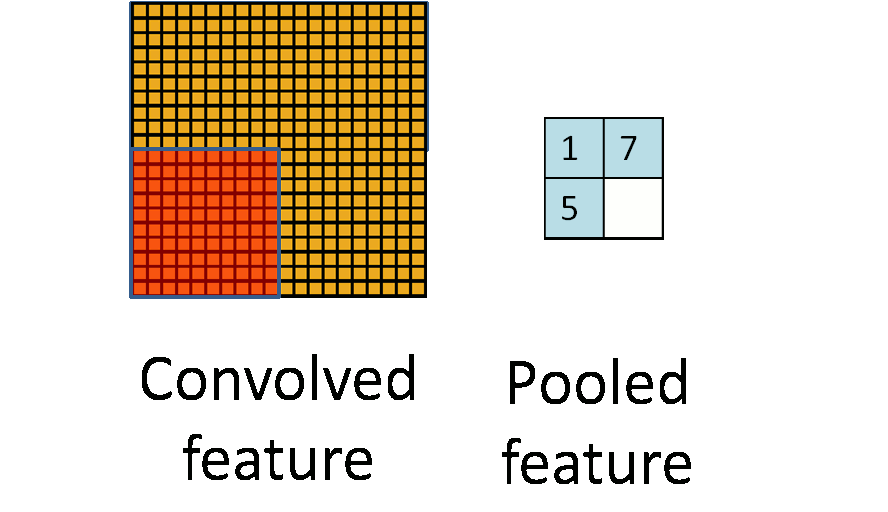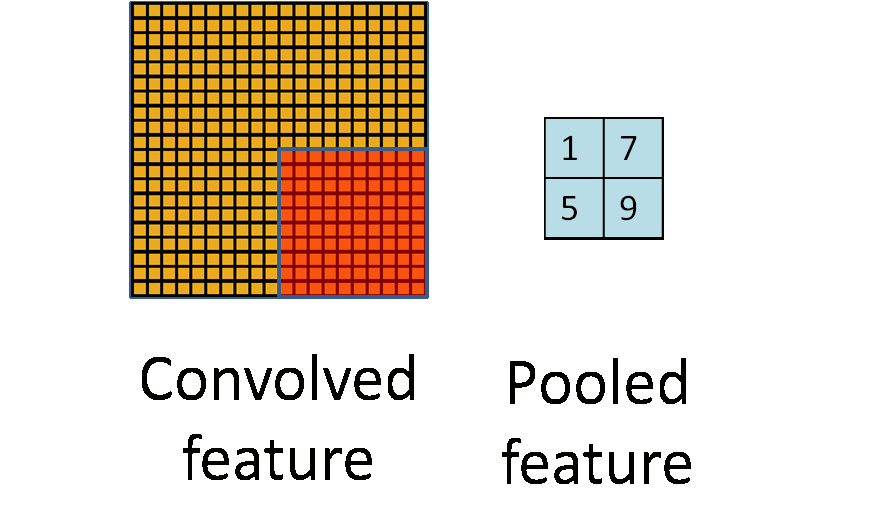
运算的定义、种类（最大池化、平均池化等）、动机。

Text-CNN的原理

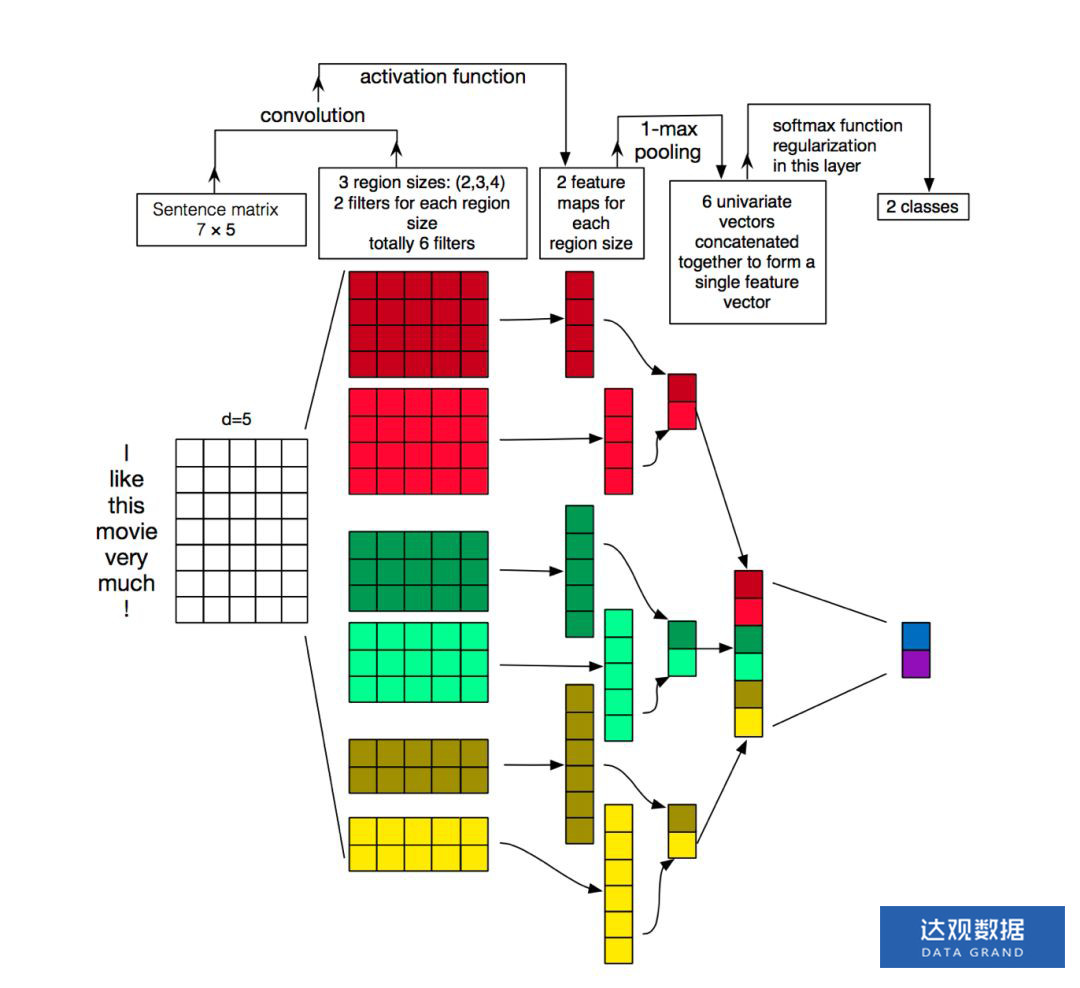
TextCNN相较于fastText模型的结构会复杂一些，在2014年提出，使用卷积 + 最大池化这两个在图像领域非常成功的好基友组合。我们先看一下他的结构。如下图所示，示意图中第一层输入为7*5的词向量矩阵，其中词向量维度为5，句子长度为7，然后第二层使用了3组宽度分别为2、3、4的卷积核，图中每种宽度的卷积核使用了两个。

其中每个卷积核在整个句子长度上滑动，得到n个激活值，图中卷积核滑动的过程中没有使用padding，因此宽度为4的卷积核在长度为7的句子上滑动得到4个特征值。然后出场的就是卷积的好基友全局池化了，每一个卷积核输出的特征值列向量通过在整个句子长度上取最大值得到了6个特征值组成的feature map来供后级分类器作为分类的依据。

图2 TextCNN结构

我们知道图像处理中卷积的作用是在整幅图像中计算各个局部区域与卷积核的相似度，一般前几层的卷积核是可以很方便地做可视化的，可视化的结果是前几层的卷积核是在原始输入图像中寻找一些简单的线条。NLP中的卷积核没法做可视化，那么是不是就不能理解他在做什么了呢，其实可以通过模型的结构来来推断他的作用。因为TextCNN中卷积过后直接就是全局max pooling，那么它只能是在卷积的过程中计算与某些关键词的相似度，然后通过max pooling层来得出模型关注那些关键词是否在整个输入文本中出现，以及最相似的关键词与卷积核的相似度最大有多大。我们假设中文输出为字向量，理想情况下一个卷积核代表一个关键词，如下图所示：

图3 TextCNN卷积核的意义示意图

比如说一个2分类舆情分析任务中，如果把整个模型当成一个黑箱，那么去检测他的输出结果，会发现这个模型对于输入文本中是否含有“喜欢”，“热爱”这样的词特别敏感，那么他是怎么做到的呢？整个模型中能够做到遍历整个句子去计算关键词相似度的只有卷积的部分，因为后面直接是对整个句子长度的max pooling。但是因为模型面对的是字向量，并不是字，所以他一个卷积核可能是只学了半个关键词词向量，然后还有另外的卷积核学了另外半个关键词词向量，最后在分类器的地方这些特征值被累加得到了最终的结果。

TextCNN模型最大的问题也是这个全局的max pooling丢失了结构信息，因此很难去发现文本中的转折关系等复杂模式，TextCNN只能知道哪些关键词是否在文本中出现了，以及相似度强度分布，而不可能知道哪些关键词出现了几次以及出现这些关键词出现顺序。假想一下如果把这个中间结果给人来判断，人类也很难得到对于复杂文本的分类结果，所以机器显然也做不到。针对这个问题，可以尝试k-max pooling做一些优化，k-max pooling针对每个卷积核都不只保留最大的值，他保留前k个最大值，并且保留这些值出现的顺序，也即按照文本中的位置顺序来排列这k个最大值。在某些比较复杂的文本上相对于1-max pooling会有提升。